Problem
Introduction
Here we
have a challenging H2 Mathematics question that tests students on the technique
of substitution, finding area and volume of solid of revolution. Note that the diagram is not drawn to scale
and the line actually intersects the ellipse (oval shape) at the point (-2,
2). Also the region R is the shaded area, but the label “R” is put outside of it. Students should do their due diligence in ascertaining
the intersection point themselves.
Solution
Remarks
Since
the word “exact” is not used in the instructions to part (iii), one can also
use the Graphing Calculator to obtain the approximate answer 3.14
to 3 significant figures. Part
(iii) can also be done by another method of integration called the Shell Method,
but this is not in the H2 syllabus.
Nevertheless, the student who uses it would not be penalised, unless explicitly
forbidden in the rubric.
The word “ellipse” means an oval shape, and is not to be confused with “eclipse” which means to occlude or hide (e.g. eclipse of the sun, eclipse of the moon). By the way, the moon orbits around the earth in an ellipse and planets revolve around the sun in ellipses (ovals).Although not part of the syllabus, it may be advantageous to know that the area of a right ellipse is pab, where a and b are the semi-axes. Imagine a circle of radius a being stretched by b/a. Then its area pa2 will be multiplied by the same factor b/a. So this is not too difficult actually. With the formula, one can verify one’s answer obtained by integration.
H02. Use a
diagram / model
H04. Look for
pattern(s)
H05. Work
backwards [ e.g. calculating new
limits for substitution ]
H09. Restate
the problem in another way
H10. Simplify
the problem
H11. Solve part
of the problem
Suitable Levels
* GCE ‘A’ Level H2 Mathematics
* IB Mathematics HL
* AP Calculus BC
* University / College calculus
* other syllabuses that involve
applications of integration
* whoever is interested


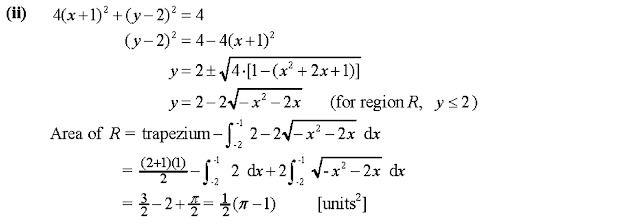

No comments:
Post a Comment
Note: Only a member of this blog may post a comment.