[OlymPri20150408CBP] Paths to avoid {#Combinatorics}

Question

Introduction

     This is an mathematics olympiad question for primary schools, and it is also a good mind-stretching exercise for students taking H2 Mathematics or IB Mathematics.  The problem can be solved using good tactics (heuristics) and some knowledge of combinations.  The number of ways to choose  r  objects out of  n  (a.k.a. “n choose r”) is 

For example, if you have  8  different balls  and you want to choose  3  out of the  8, the number of combinations is  ⁸C₃ = 56.   You write 8 on top and 3 below and then introduce new factors by successively decreasing each number by one, until the bottom factor reaches 1.  Notice that the number of factors in the numerator is equal to the number of factors in the denominator.

     Sometimes, ⁿC_r is written like a  2 by 1  column vector.  Many teachers introduce the concept with a formula using factorials, but the above formula is more practical for calculations.  Combinations have a nice symmetrical property.  For example, ⁸C₅ = ⁸C₃ = 56.  Why?  That is because choosing  5  objects out of  8  is the same as choosing  3  to be rejected.  This can be verified by writing  ⁸C₅  out in full and cancelling the factors.

Solution

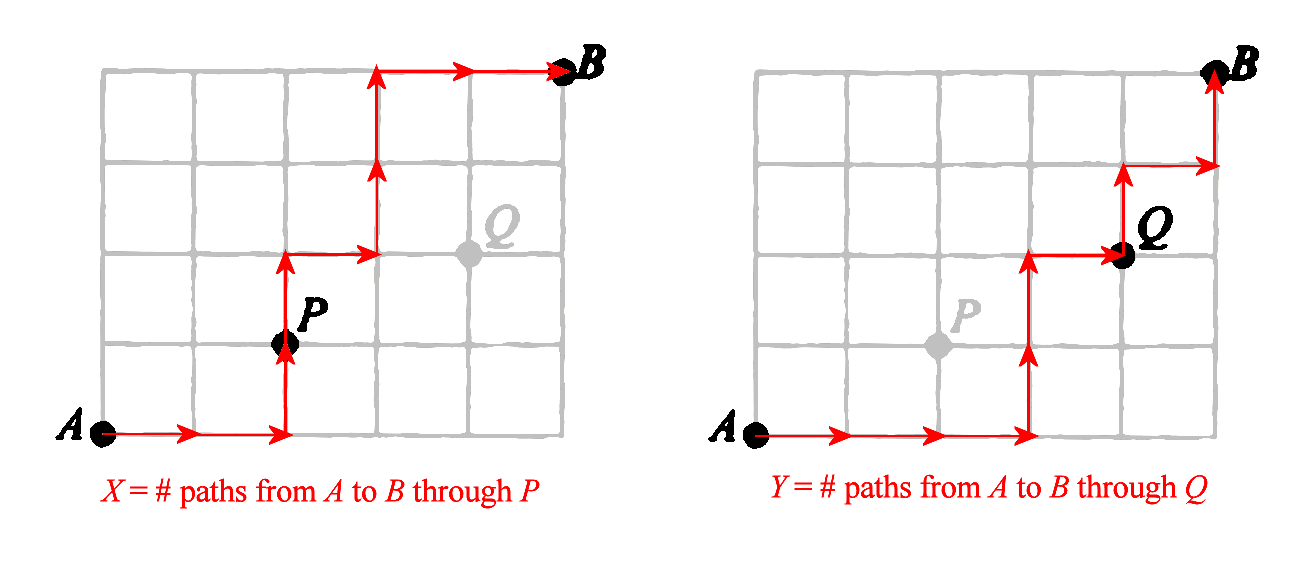
     First, let us note that every path from  A  to  B  is equivalent to a sequence of right arrows (®) and up arrows (á).  In the above example, the path corresponds to a sequence “®áᮮᮮá”.  There are  9  symbols in each sequence, of which  5  must be “go right” and  4  must be “go forward”.  [H12* Think of a related problem]  The number of such paths is
          W = # of paths from  A  to  B  = ⁹C₄  = ⁹C₄  =  126.

However, we do not want the paths that pass through  P  or  Q.  So we need to consider

          X = # of paths from  A  to  B  passing through  P

          Y = # of paths from  A  to  B  passing through  Q

The problem is, if you added these, the paths that pass through  P  and  Q  would have been double-counted.  So we also need to consider

          Z = # of paths from  A  to  B  passing through  P  and  Q

The required number of paths would be  W – (X + Y – Z) = W – X – Y + Z.  Let us calculate part by part.

          X = # of paths from  A  to  B  passing through  P

             = (# of paths from  A  to  P) ´ (# of paths from  P  to  B)

             = ³C₁ ´ ⁶C₃  = 3 ´ 20 = 60

          Y = # of paths from  A  to  B  passing through  Q

             = (# of paths from  A  to  Q) ´ (# of paths from  Q  to  B)

             = ⁶C₂ ´ ³C₂  = 15 ´ 3 = 45

          Z = # of paths from  A  to  B  passing through  P  and  Q

             = (# paths A  to  P) ´ (# paths  P  to  Q) ´ (# paths  Q  to  B)

             = ³C₁ ´ ³C₁ ´ ³C₂  = 3 ´ 3 ´ 3 = 27

The paths from  A  to  P  are chosen independently from the paths from  P  to  B.  That is why we are able to multiply the numbers.  Likewise, the other multiplications are justified because of independence.  Putting everything together,

                 # of paths from  A  to  B  passing through neither  P  nor  Q

             = W – X – Y + Z = 126 – 60 – 45 + 27 = 48   J

Heuristics Used

H02. Use a diagram / model

H09. Restate the problem in another way

H10. Simplify the problem

H11. Solve part of the problem

H12* Think of a related problem

Suitable Levels

* GCE ‘A’ Level H2 Mathematics (“Permutations and Combinations”)
*  IB Mathematics HL / SL (“Counting Principles”)
* Primary School Mathematics Olympiad
* anyone, young or old, who is interested in thinking